Probability Puzzles

Problem Statement

How many cards would you expect to draw from a standard deck before seeing the first ace?

Solution

Let’s consider an experiment where we’re pulling cards from a shuffled deck till we get the first ace. This experiment has only 49 possible outcomes – we’re guaranteed to see the first ace between 1st and 49th attempts. We can say that a random variable X representing outcomes of this experiment possesses integer values in the interval [1 ; 49].

Let’s calculate the probability to pull an ace on various attempts:
P(X = 1) = 4 / 52
P(X = 2) = (48 / 52) * (4 / 51)
P(X = 3) = (48 / 52) * (47 / 51) * (4 / 50)

For P(X = 2) we didn’t pull an ace on the first attempt (48 / 52), but we got it on the second (4 / 51). The denominator decreased since on the second attempt we’re pulling from 51 cards. Following the same logic, P(X = n) would be:

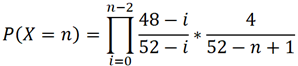
Now we need to find the expected value of X which is:

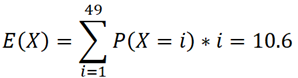
Getting back to the initial question – “how many cards would you expect to draw from a standard deck before seeing the first ace” – we’d need to subtract 1 from the above value, i.e. it would be 9.6

Not convinced? Try the simulation below!

Simulation

show / hide simulation code

import random

nrounds = 1000
cards_before_first_ace = 0

# Deck with 1 representing an Ace
deck = list(range(1, 14)) * 4

for _ in range(nrounds):
    random.shuffle(deck)

    for i in range(0, 49):
        if deck[i] == 1:
            cards_before_first_ace += i
            break

simulated_probability = round(cards_before_first_ace / nrounds, 4)